Ce module définit et met en relation les nombres trigonométriques d'un angle aigu d'un triangle rectangle. Les valeurs particulières, les propriétés fondamentales de ces nombres trigonométriques y sont établies. Il aborde également la notion de pente, d'angle de pente, la résolution de triangles. Vous résoudrez quelques cas concrets.
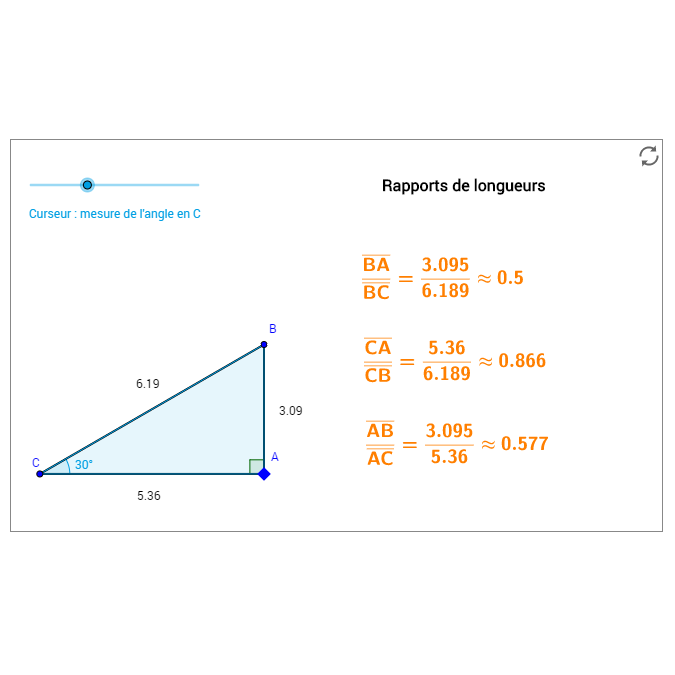
Ce module est consacré à la résolution de triangles quelconques à l'aide de la règle des sinus et de la règle des cosinus (aussi appelée théorème d'Al-Kashi ou théorème de Pythagore généralisé). Les cas concrets sont privilégiés.
Ce module est consacré à la résolution des équations trigonométriques. Les procédures de résolution sont présentées en fonction d'un classement des équations : équations fondamentales, équations factorisables, équations se ramenant au second degré, équations du type a.cos x + b. sin x = c.
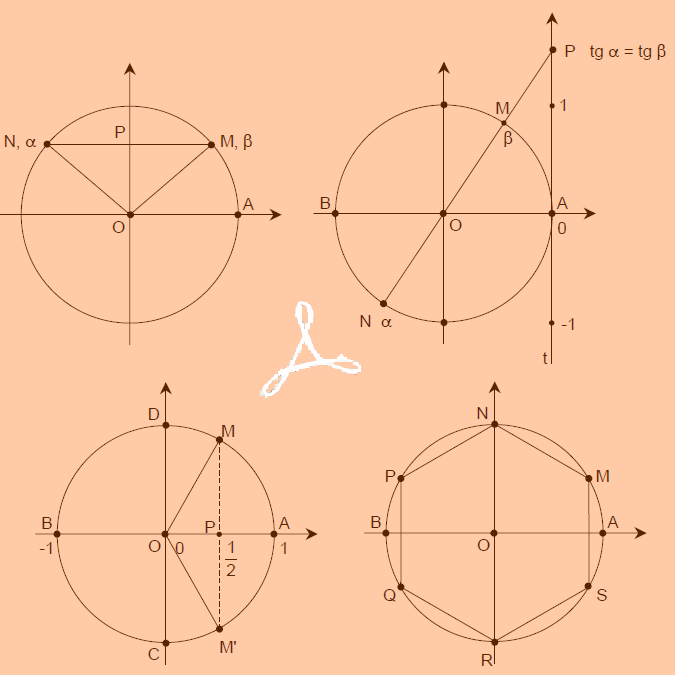
Ce module est consacré à l'étude des relations entre les nombres trigonométriques des angles et la transformation d'expressions trigonométriques. Les relations entre les nombres trigonométriques des angles s'établissent au moyen des formules d'addition, formules de duplication, formules de Carnot et de Simpson. Ces formules permettent aussi d'élargir la gamme des angles particuliers (22°30', 15°, 75°, …).
Ce module est consacré aux fonctions sin x, cos x, tg x et cotg x. L'interprétation de chaque fonction à l'aide du cercle trigonométrique conduit progressivement aux graphiques et aux propriétés. Pour chacune de ces fonctions, la définition, la représentation graphique, les valeurs extrêmes, la période, les racines, la parité sont abordés avec leur interprétation sur le cercle trigonométrique et sur le graphique de la fonction.
Ce module est consacré à la résolution de triangles quelconques à l'aide de la règle des sinus et de la règle des cosinus (aussi appelée théorème d'Al-Kashi ou théorème de Pythagore généralisé). Ces propriétés sont démontrées. Quelques cas concrets sont étudiés.
Ce module est consacré à la trigonométrie dans un cercle appelé trigonométrique. Il aborde les angles orientés, la définition du cercle trigonométrique, ses quadrants et la mesure principale d’un angle orienté, les nombres trigonométriques et quelques valeurs remarquables, dans ce cercle. Les angles associés (complémentaires, opposés, supplémentaires, anti-supplémentaires) y sont utilisés pour la simplification d'expressions.